通常,自编码这个任务都是通过CNN,MLP等神经网络来实现。周志华教授在论文中表示,他们提出了一种算法可以使森林能够利用决策树决策路径(decision paths)定义的等效类别来进行反向重构(backward reconstruction),并且证明了这种算法在监督学习和无监督学习的可行性。
简单介绍一下什么是Autoencoder
网络结构:对于所有的自编码器来说,目标都是样本重构。
自编码器首先通过encoder(编码层)把高维空间中的向量x,压缩成低维向量z(中间向量或潜向量),然后通过解码层把低维向量解压重构出x。如下图所示:
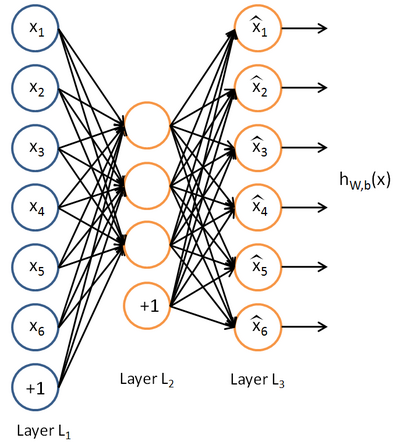
如图标准的autoencoder,目标仅仅是降维,重构样本,最后使用训练好的中间层(可以连接softmax用作分类等),这种ae包括稀疏自编码、栈式自编码、去噪自编码。
变分自编码器(VAE):不一样的autoencoder,用作生成数据。
我们想一下普通的AE可以生成数据吗?回答必然是肯定的,但是这种数据只不过是隐向量解码得到与原图对应的图(并不能任意生成!!!),也就是说我们不知道Z服从什么样的分布函数,并不能生成新的样本。那么我们可否自己去构造隐藏向量? 于是,聪明的人类发明出VAE.
原理:在编码过程中给它进行一些限制,迫使生成的隐含向量能够粗略的遵循一个高斯分布,这也是与一般的autoencoder最大的不同
这样我们生成一张新的图片就很简单了,我们只需要给它一个标准正态分布的随机隐含变量。这样一旦我们网络训练完毕后,我们就可以从高斯分布中采样一个样本解码生成样本。
与GAN对比:
- 由于它们所遵循的是一种 编码-解码 模式,我们能直接把生成的图像同原始图像进行对比,这在使用GAN时是不可能的。
- 由于它是直接采用均方误差而非对抗网络,其神经网络倾向于生成更为模糊的图像。
Eforest
对于森林来说,编码是没有困难的,因为至少叶节点信息就可以被认为是一种编码方式,并不用说路径分支,节点的子集等都能提供更多的编码信息。
Eforest编码过程:

编码过程并不复杂,一旦遍历完所有的树,就会返回T维向量,其中for循环中的每个元素i都是对应树的叶节点的整数索引
解码过程:
解码过程就不那么明显了,实际上,森林通常从树的根节点到叶子节点前向预测,而反过来重建规则就不是很清楚了。例如:如何通过叶子获得的信息合成原始的样本。
假设我们正处于四个属性的二元分类。第一个和第二个属性是数字属性,第三个是布尔属性,值为YES或者NO;第四个为颜色属性分别为:RED、BLUE、GREEN。给定一个对象x,令xi表示x的第i个属性的值。
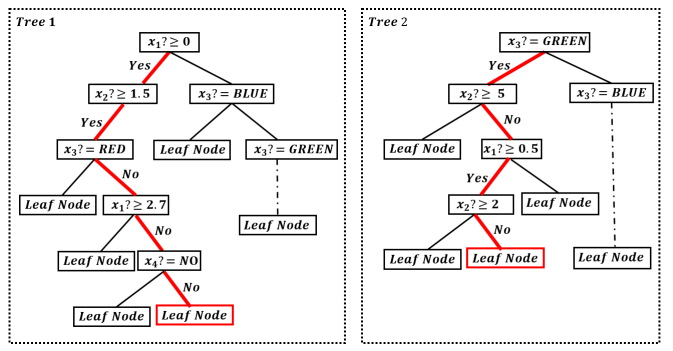
假如编码步骤中,我们生成了上图Tree1,2,…这种森林。现在我们只知道对象x所在叶节点即红色节点,我们希望重构x。周志华教授提出了一个有效并且简单的向后重建策略。
首先每个叶节点都对应一个来自根节点的路径,在上图中,识别出来的路径用红色突出显示(随机)。每个路径对应以下规则集:
RULE1:(x1≥0)∧(x2≥1.5)∧┐(x3==RED)∧┐(x1≥2.7)∧┐(x4==NO)
RULE2:(x3==GREEN)∧┐(x2≥5)∧(x1≥0.5)∧┐(x2≥2)
…
RULEn: (x4==YES)∧┐(x2≥8)∧┐(x1≥1.6)
化为更一般的形式:
RULE1’: (2.7≥x1≥0)∧(x2≥1.5)∧┐(x3==RED)∧(x4==YES)
RULE2’: (x1≥0.5)∧┐(x2≥2)∧(x3==GREEN)
…
RULEn’: ┐(x1≥1.6)∧┐(x2≥8)∧(x4==YES)
然后就可以推导出最大相容规则MCR。MCR规定:每个成员的覆盖范围都不能被放大,否则就会发生不兼容问题。
RULE1…RULEn这种规则集可以的得到MCR规则:(1.6≥x1≥0.5)∧(2≥x2≥1.5)∧(x3==GREEN)∧(x4==YES)
在获得MCR以后,我们才开始重建原始样本。对于x3,x4的属性MCR必须取这些值中之一;对于数值属性,我们可以选择其中具有代表性的值,如(2,1.5)中的平均值(也可以选择中值,最大值,最小值)。
因此重建以后的属性就是x=[1.05,1.75,GREEN,YES]
于是我们eFoerst的解码过程如下所示:
- 给定一个训练好的T棵树的森林具体来说,,同时对一个特定数据,有 RT(T 为上标)中的前向编码 xenc(enc 为下标)。
- 后向解码将首先通过 xenc 中的每个元素定位单个叶节点,然后对于对应的决策路径,获得相应的 T 个决策规则。
- 计算 MCR,我们可以将 xenc 返回给输入区域中的 xdec。算法3中给出了具体的算法。

这篇文章eforest结构到这就结束了。经过实验证明(原文链接),eForest 除了在精度和速度方面都表现良好,以及具备一定的鲁棒性之外,还能够重复使用。需要特别指出的是,在重建文本数据时,仅仅需要 10% 的输入位(input bits),该模型依然能够以很高的精度重建原始数据。
